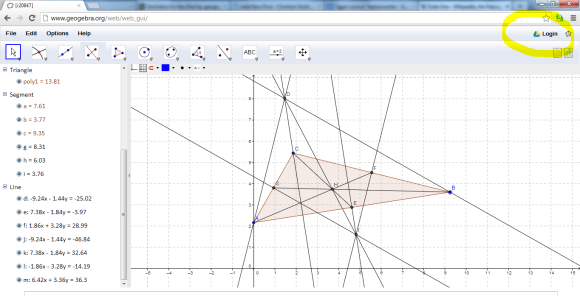
The third session I attended was more a discussion and critique session, led by Monaghan and Mason, on the topic of ‘cultural affordances’. The basis was the work of Chiappini, who -in the ReMath project- used the software program Alnuset (see here to download it) to look at (its) affordances. Monaghan described the work (a paper on the topic, there will be a publication in 2013, was available) and then asked some questions. Chiappini distinguishes three layers of affordances: perceived, ergonomic and cultural. Engestroms cycle of expansive learning is used, as I understood it, to use activities as drivers for transformation of ergonomic affordances into cultural affordances. Monaghan then asked some critical questions, under which whether the theory of Engestrom really was necessary, wouldn’t for example Radfords work on gestures be more appropriate? Another comment pondered whether the steps for expansive learning were prescriptive or descriptive. I think the former: as the author has made the software with certain design elements in mind it is pretty obvious that they have a preconceived notion of how student learning should take place. It was pretty hard to discuss these more philosophical issues in detail. I’m not really sure if I even understand the work. Although this could be solely because I haven’t read enough about it, I also feel a bit as if ‘difficult words’ are used to state the obvious. I could only describe what I was thinking off. The article that I took home afterwards gave some more pointers. To get a grasp of this I downloaded the software, that reminded me a bit of the Freudenthal Institute’s ‘Geometrische algebra’ applets, and tried out the software. I liked the idea behind the software. In this example I’ve made three expressions, and I can manipulate x. The other two expressions change with x. Some comments:
it is pretty obvious that they have a preconceived notion of how student learning should take place. It was pretty hard to discuss these more philosophical issues in detail. I’m not really sure if I even understand the work. Although this could be solely because I haven’t read enough about it, I also feel a bit as if ‘difficult words’ are used to state the obvious. I could only describe what I was thinking off. The article that I took home afterwards gave some more pointers. To get a grasp of this I downloaded the software, that reminded me a bit of the Freudenthal Institute’s ‘Geometrische algebra’ applets, and tried out the software. I liked the idea behind the software. In this example I’ve made three expressions, and I can manipulate x. The other two expressions change with x. Some comments:
- I like the way expressions are made and the look and feel, as well as the way dragging changes the expression. Also ‘dividing by zero’ causes expressions to disappear. However, why does x=0 disappear as well when I drag x to 0? (see figure)
- I don’t see how the drawback of every tool that allows ‘dragging’, namely just pointless dragging, in this case just to line up the different expressions, is solved. Maybe this isn’t the main goal of the software.
- I think that the number line should be used in conjunction with tables and graphs, thus forming a triad expression-table-graphs. The addition of things like an algebraic manipulator and a Cartesian plane seems to indicate that the authors also like more than one representation.
- It has far too limited scope for algebra. The 30 day trial is handy here, as in my opinion the software doesn’t do enough to warrant the price.