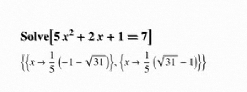Only recently I read this blogpost on a TED talk by Conrad Wolfram.
Although I agree with most in the blogpost, I think Wolfram paints a caricature of mathematics. Let me make some comments.
I think Wolfram generalizes too much with regard to different countries. I don’t really know that much about the US situation, but I have the impression that procedural fluency and computation are valued much more over there than in Asia or Europe. Something that Michael Pershan also points out in this excellent video. In the Netherlands conceptual understanding is deemed more important, as is the connection to the real world. In this respect Wolfram exaggerates the percentage involved in computation (80% computation by hand).
This brings me to another point. Wolfram is highly involved with some of the developments of Mathematica software (which his brother Stephen created). He even shows it off in his talk. Undoubtedly, Mathematica and Wolfram Alpha are great pieces of software, that can perform awesome calculations. This, however, makes clear that that using a tool to get rid of computation is what is central in his talk, not the other three points.

Mind you, these three steps are very important, and remind me of Polya on problem solving. I just don’t agree with Wolframs fixation on discarding the third point. Wolfram does see a place for teaching ‘computation’ and says we “only [should] do hand calculations where it makes sense”. He also talks about what ‘the basics’ are, and makes a comparison with technology and engineering in cars. Here it would have helped if Wolfram would have acknowledged the difference between blackbox/whitebox systems (see Buchberger, http://dl.acm.org/citation.cfm?id=1095228):
In the “white box” phase, algorithms must be studied thoroughly, i.e. the underlying theory must be treated completely and algorithmic examples must be studied in all details. In the black box phase, problem instances from the area can be solved by using symbolic computation software systems. This principle can be applied recursively.
The whole section where Wolfram addresses criticims of his approach sounds far too defensive. He does not agree with the fact that mathematics is dumbed down, and using computers is just ‘pushing the buttons’. This has to do with the traditional discussion between ‘Use to learn’ and ‘Learn to use’. Again, I think Wolframs whole argumentation is a bit shaky: first he attacks learning algorithms with pen-and-paper , but then he does see a fantastic use regarding understanding processes and procedures. This is where Wolfram applauds programming as a subject. Then he shows many applications with sliders and claims: Feel the math! He shows an application for increasing the sides of a polygon and claims this introduces the “early step into limits”. By using a slider? I’m thinking of an applet I used in my math class teaching the concept of slopes and differentation. I thought it worked pretty well…until I found out students were just dragging the two points together. So what is actually learned?
As another example, there is a part where Wolfram subtitutes the power 2 with a 4, uses Mathematica, and then says ‘same principles are applied’.
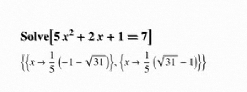

If he means that the same piece of software was used, then this is the same principle. If his claim is that the mathematics behind solving an higher order equation uses the same principles as solving a quadratic equation, then I wonder if this really is the message you want to convey to students. Of course the outside world has much more difficult equations, and that brings me to a final point made, concerning a ‘means to an end’. Wolfram does not define what the actual goal of mathematics is. If it is ‘getting the result’ then one could argue that using a computer over doing it by hand makes sense. However, if -and that was Wolframs claim- the goal is ‘teaching’ then I think mathematics brings more than just some results. Wolfram seems to see mathematics as a supporting science for other subjects, and does not seem to acknowledge a broader view of mathematics as a subject aimed at problem. Which is strange regarding Wolframs initial words on really teaching mathematics.
By no means I’m claiming this is an overly extensive critique of Wolfram’s talk, just a few points that -to me- warrant the conclusion that Wolfram paints too much of a caricature of maths education. I’d rather keep it with the conclusion of the blogpost it started with (translation): “Put aside those textbook with tasks, en tell students what has inspired you to learn your subject. Tell stories. Or get people into the classroom to show inspring examples. Let students look at problems in a different way, and see how they can address these problems with the help of mathematics.”. Amen.
can be done by using the rule for exponents
and so if
then
. But you could also say that, just like
,
could be assumed when proven. If you would state: ‘but I want
to be proven from the most basic rules and assumptions’ this seems a fair request.
but that
is enough. Because let
then
which is (under this law)
. So
and so
must be 1.
. Actually I don’t really care whether you prove it or not, but I do think some ‘feel’ for assumptions, axioms, dependencies etc. is useful for everyone. This was the only point I was trying to make.
which is indeterminate.
in Wolfram and in Google. But there are other views, like this one stating that
and also the Math Forum has some interesting quotes.